Project 2: Fun with Filters and Frequencies!

This section explores filters and how we can manipulate images utilizing frequency. In regards to the gradient magnitude computations, I first convolve the image with the filter [1, -1] to get the x component, Gx, of the gradient. Then I convolve with [[1], [-1]] to get the y component of the gradient, Gy. Afterwards, I compute the square root of the sum of squares of the x and y components of the gradient to get the gradient magnitude, sqrt( G_x² + G_y² ). The most important thing I learned from this project is the importance of reading documentation as some plotting libraries treat image channels in a different order. Additionally, I also realized the importance of having organized and modular code.

For this section, I create a smoothing filter from the Gaussian Filter which I made by taking the dot product with itself from a 1D Gaussian filter. I also convolve the gaussian with Dx and Dy and it gives the same result.

Gaussian Filter Result: The edge image has less artifacts from the grass and the edge are more clearly extracted. The edges that were detected from the grass no longer show up after we convolve with the Guassian filter. The edges are cleaner and there is less noise.

Derivative of Guassian Filter Result: This is the same result as the previous images showing that can do the same thing with a single convolution by creating a derivative of gaussian filters.

For this section, I low pass filter the image. Then I subtract that low frequency image from the original image to get the high frequency components of the image. Then I add a small portion of the high frequency image back to the original since images look sharper if it has stronger high frequencies.

We can see that blurring a sharp image and then sharpening it gives back the original image. However, there are some artifacts, but the edges are improved from the blurred image.

This also shows that blurring a sharp image and then resharpening it does a good job of restoring the quality of the image.

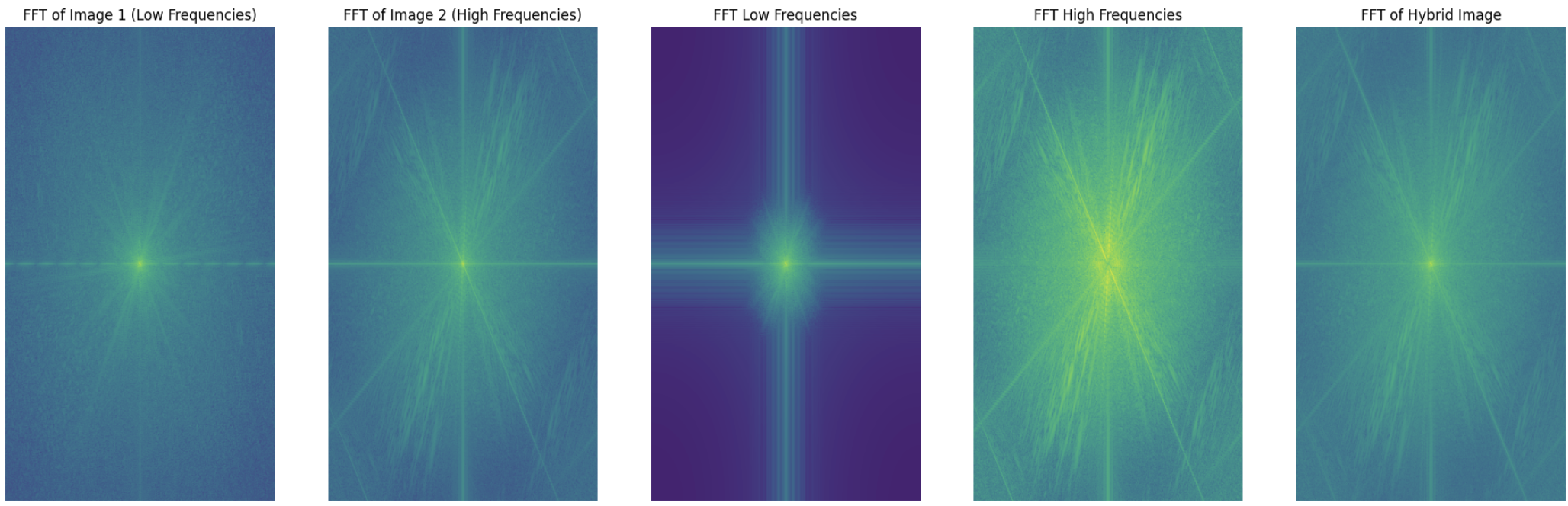
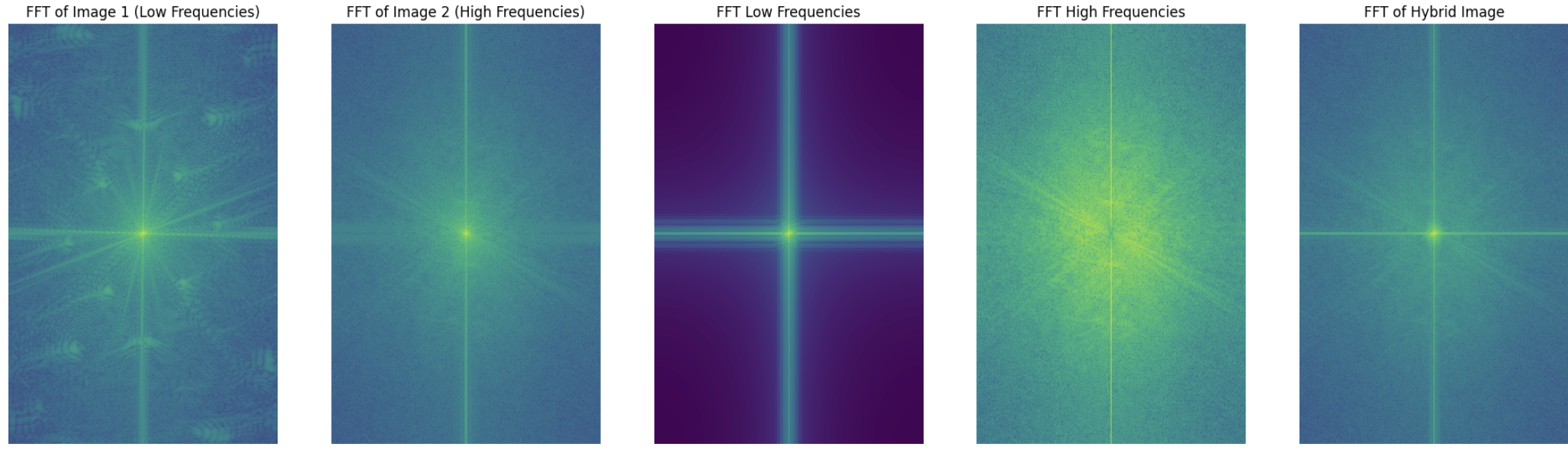
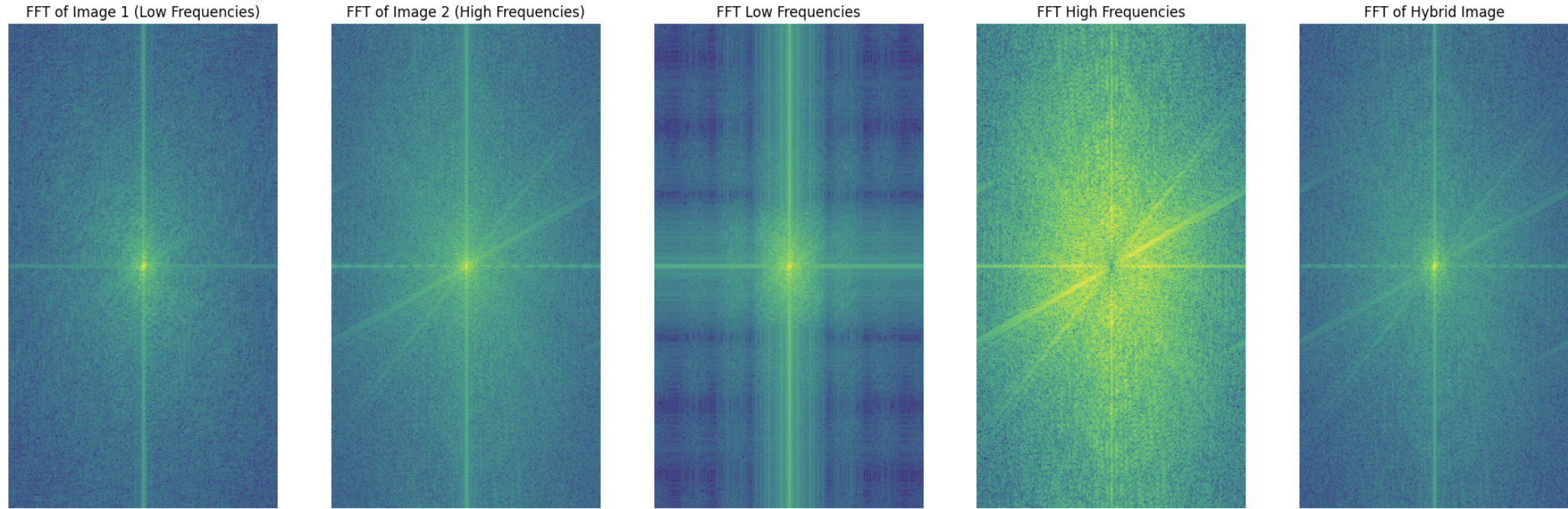
In order to create hybrid images, I low pass one image and high pass filter another image (by subtracting the low frequencies) and then combine the images. I set thresholds appropriately in order to get the desired effect.

Sahai and Louis XIV

This hybrid image failed and did not work as well as the rest. This is most likely due to the two figures in the picture being at different orientations as well as the big difference in resolution between the two images. Additionally, one of the images is from a painting which may have impacted the processing.

In order to make Gaussian stacks I repeately apply Gaussian blur to the previous image in the stack. To make the Laplacian stack I take the ith image in the Gaussian stack and subtract the i+1th image from the Gaussian stack from it.

In order to blend images, I make a Laplacian stack for both images. Then I create an appropriate mask that defines the blending boundary. Then I apply Gaussian blur to the mask and create a Gaussian stack. Then I use the algorithm from the 1983 paper. This algorithm iterates through the stacks and element wise multiples the mask with the first images Laplacian stack image and then adds that to (1 - mask) element wise multipled by the second images Laplacian stack. Then, we sum over all the stacks to get the final image.

Oraple Blending

Track Teammates Blending

Irregular Mask for Boy and Cat blending.

Boy and Cat Blending with Irregular Mask